Resolver gráficamente el siguiente sistema de ecuaciones
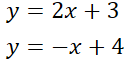
Para dibujar cada recta, se prepara una tabla x , y. En la cual se escriben 3 valores para x. Los valores pueden ser cualesquiera, sin embargo, se propone poner números sencillos, como ser 0, 1 y 2. Luego se reemplaza dichos números en la ecuación y se obtiene los valores de y correspondientes.
![]()
y = 2x0+3 = 3
y = 2x1+3 = 5
y = 2x2+3 = 7
|
x |
y |
|
0 |
3 |
|
1 |
5 |
|
2 |
7 |
y = -x + 4
y= -0 + 4 = 4
y= -1 + 4 = 3
y= -2 + 4 = 2
|
x |
y |
|
0 |
4 |
|
1 |
3 |
|
2 |
2 |
Una vez que tenemos 3 puntos en cada tabla graficamos
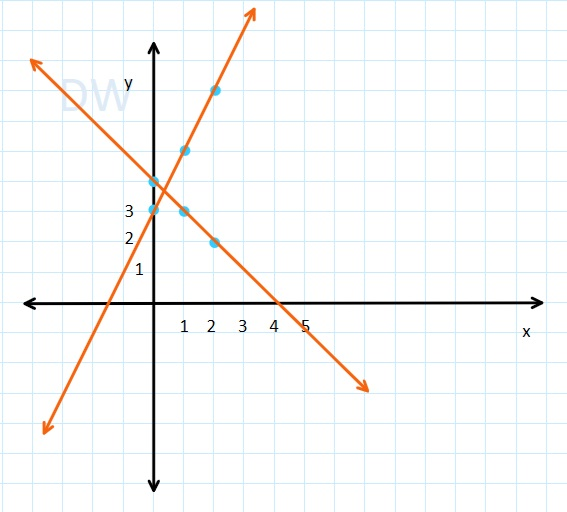
La respuesta queda determinada por el punto de intersección. En este caso es aproximadamente (0,3 ; 3,6)
No es necesario pero si muy útil verificar la solución obtenida. Sirve para comprobar que el resultado obtenido es correcto. No necesitamos entregar el ejercicio para que el profesor lo corrija. Ya podemos determinar nosotros si está correcto. Y si no lo está, da la posibilidad de encontrar el error y corregirlo. Para verificar, se reemplaza en las ecuaciones, la respuesta obtenida.
verificación
y= 2x+3 = 2*0,3+3=3,6
y= -x+4 = -0,3+4=3,7
Se puede observar que la respuesta es casi la misma. Los valores son aproximados y por eso no coinciden exactamente.
Por lo explicado, la respuesta al ejercicio es aproximadamente x=0,3 e y= 3,6
Ahora veremos otro ejemplo. En este, no tendremos las y despejadas. O sea, no se encontrarán las y de un lado de la ecuación y las x del otro.
2x+5y=26
-3x+4y=7
Lo primero que podríamos hacer es despejar las y. Para ello, necesitamos transponer, pasar, primeros los términos que están sumando y que acompañan a las y. El nuevo sistema quedaría así.
5y= -2x + 26
4y = 3x + 7
Y ahora, como las y están acompañadas de coeficientes que están multiplicando, los podemos transponer, pasar al otro lado, dividiendo por ellos. Y el sistema de ecuaciones quedaría así.
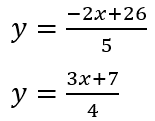
Ahora, si, podemos preparar las tablas x , y. Donde asignaremos valores a x y obtendremos los correspondientes valores de y. Le podemos asignar a x, los valores que dimos en el ejemplo anterior, 0, 1 y 2.
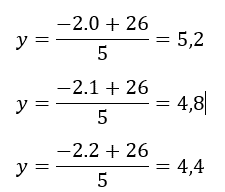
Y, en este caso los resultados nos dan con decimales. No obstante, podemos buscar, valores más convenientes como ser -2, 3 y 8. Obteniendose
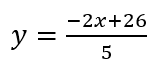
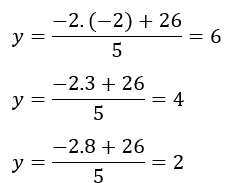
|
x |
Y |
|
-2 |
6 |
|
3 |
4 |
|
8 |
2 |
Tomando la segunda ecuación, buscamos valores cómodos para graficar
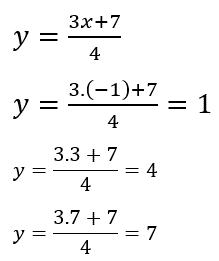
Y hacemos la tabla correspondiente
|
x |
Y |
|
-1 |
1 |
|
3 |
4 |
|
7 |
7 |
Ahora, ya podemos graficar ambas tablas en un mismo gráfico.
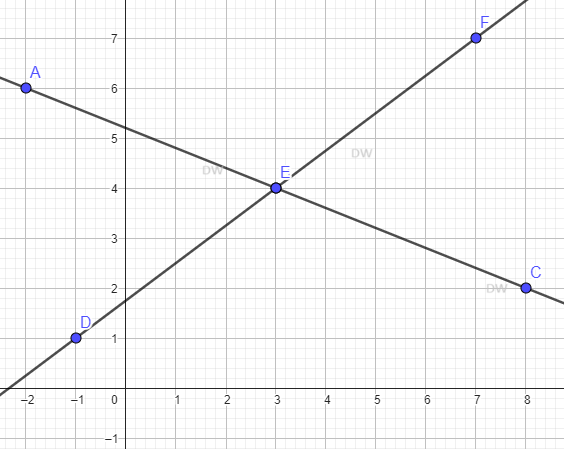
Ambas rectas se cortan en x=3 e y=4.
Luego, verificamos la solución obtenida. Y reemplazamos la solución en el sistema inicial.
2x+5y=26
-3x+4y=7
2*3+5*4= 26
26=26
-3*3+4*4=7
7=7
Con lo cual se ha verificado la solución




