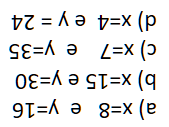Luego de los ejemplos, hay ejercicios con sus respuestas para quienes quieran practicar. Este es el primero de una serie articulos sobre este tema.
Ejemplo 1
![]()
Dado que las y se encuentran despejadas puedo igualar ambas expresiones directamente. El paso que pondré ahora, no es usual ponerlo ni se necesita, pero, evidenciará porque se pueden igualar.
![]()
Ahora, ya contamos con una sola ecuación que tiene una sola incógnita. Y podemos pasar la x que está sumando al otro miembro, realizando la operación contraria, restar.
![]()
Ahora, tenemos que restar los terminos que tienen x.
![]()
Y así, ya tenemos la solución para x. Ahora, tenemos que obtener el valor de y. Para ello, reemplazamos en cualquiera de las 2 ecuaciones iniciales el valor obtenido de x, en la posición dónde está la x
![]()
Ya tenemos ambas respuestas. No obstante, para terminar el ejercicio resulta útil reemplazar el valor obtenido de x, en la ecuación no utilizada para verificar que se obtiene el mismo valor de y.
![]()
Se ve que el valor calculado para y es el mismo en ambos cálculos, 10. Lo cual muestra que se realizó, correctamente, el ejercicio. Siendo la respuesta del problema x=5 e y=10
Cuando antes escribí "que las y se encuentran despejadas" expresé que están solas. No tienen nada que las multiplique, divida, sume o reste. El miembro se compone unicamente de una y.
Ejemplo 2
Aumento un poco la dificultad del siguiente sistema de ecuaciones
![]()
Nuevamente, las y están despejadas y aprovechamos ello, para igualar las ecuaciones
![]()
Volvemos a agrupar las x en un mismo miembro.
![]()
Y volvemos a restar las x
![]()
Ahora, nos encontramos con otra dificultad que no surgió en el ejemplo anterior. La x no se encuentra despejada. Esta acompañada por un número, un coeficiente, distinto de 1. Y, necesitamos despejar la x. Requerimos que la x se encuentre sola. Para ello, pasamos el 3 al otro miembro, con la operación contraria a la que está ejerciendo. Está multiplicando, entonces, pasa dividiendo.
![]()
Ya tenemos el valor de x, ahora, reemplazamos en ambas ecuaciones para tener el valor de y. Y, para verificar que no nos hayamos equivocado.
![]()
Ambas ecuaciones mostraron que y=12. Validando la resolución del ejercicio. Siendo entonces, la respuesta x=3 e y=12
Ejemplo 3
![]()
Igualamos ambas ecuaciones
![]()
Pasamos las x a un solo miembro y restamos
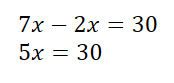
Despejamos la x, transponiendo el coeficiente que tiene, que la acompaña.
![]()
Reemplazamos el valor obtenido en las ecuaciones iniciales
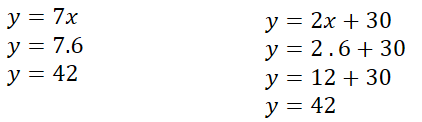
Ambas ecuaciones dieron el mismo valor para y. Se resuelve y verifica así el sistema. Resultando x=6 e y=42
Ejercicios
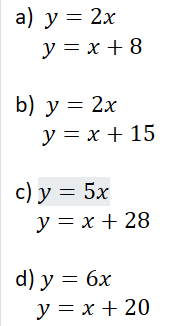
En siguientes artículos, continuaremos aumentando la dificultad de los sistemas de ecuaciones.
Respuestas a los ejercicios dados