
En matemáticas es algo bastante común contar con diferentes funciones que sirven para obtener resultados a un problema específico. Una de las operaciones matemáticas que puedes encontrar con frecuencia es la progresión geométrica.
Este tipo de operaciones matemáticas pueden llegar a ser bastante complejas para algunas personas. Y es que no todo el mundo cuenta con un buen entendimiento de las matemáticas. Sin embargo, las progresiones geométricas son mucho más sencillas de lo que imaginas.
En cualquier caso, si te parecen muy difíciles estas operaciones matemáticas, lo más recomendable es que cuentes con un tutor. Con la ayuda de uno, los ejercicios de progresión geométrica serán pan comido.
Si requieres de uno, en Busca Tu Profesor podrás encontrar los mejores tutores profesionales. Encontrarás una gran cantidad de profesores de matemáticas que podrán ayudarte. Además, contratar a un tutor puede llegar a ser bastante más económico de lo que puedas imaginar.
¿Qué es una progresión geométrica?
Una progresión geométrica es una secuencia que se encuentra formada por varios elementos sucesivos. Estos se obtienen mediante la multiplicación del elemento por un valor constante. En ese caso, esta constante se le conoce como factor o razón.
En general, estas progresiones son una secuencia con un número finito de términos. En el caso de que la secuencia pueda extenderse hasta el infinito, entonces se habla de una sucesión matemáticas geométrica.
Pongamos un ejemplo de esto: en el caso de una progresión geométrica cuyo factor es 5, tenemos que serían los siguientes: 5, 25, 125, 625, 3125, 15625. En este caso, como se puede apreciar, la progresión se da multiplicando cada término por 5. El resultado es la progresión geométrica que hemos descrito.
Probablemente visto de esta manera, te parezca un poco difícil comprender cómo funcionan las progresiones geométricas. Sin embargo, una vez que empieces a practicarla, te darás cuenta de que es mucho más sencillo de lo que puedas imaginarte.
Leer más: Lista de profesiones con más futuro
¿Para qué sirven las secuencias matemáticas?
Las secuencias numéricas o secuencias matemáticas son algo muy importante en nuestro día a día. Estas se caracterizan por permitir que las personas puedan seguir una secuencia numérica y determinar qué número sigue.
Pongamos un ejemplo sencillo, si vas a visitar a un amigo en un edificio y este cuenta con 10 pisos, pero tu amigo vive en el séptimo. Una secuencia numérica te va a permitir determinar a cuál piso deberás ir.
Ejemplos similares puedes encontrarlos en tu día a día y en cualquier momento. Es por ello por lo que las secuencias numéricas son tan importantes y la razón por la cual debes entenderlas, aprenderlas y ponerlas en práctica.
Como ya mencionamos, una buena forma de aprender sobre secuencias matemáticas es contratando a un tutor profesional. Puedes conseguir a alguno de estos tutores en Busca Tu Profesor a un precio bastante asequible.
¿Cómo entender cuál es la esencia de una progresión geométrica?
Muchas personas se preguntan cuál es la esencia o la importancia de una de estas operaciones. Lo cierto es que, estas son sumamente importantes, especialmente en el mundo de los negocios donde son muy utilizadas.
Son ampliamente utilizadas en el mundo de las inversiones, estas permiten determinar intereses. Es por ello por lo que, aunque creas que estas no tienen demasiado uso en el mundo real, lo cierto es que se usan más de lo que crees.
Leer más: ¿Qué es una plataforma de búsqueda de profesor en línea? Descripción de las plataformas más populares en España
Fórmulas de progresión geométrica: ejemplos
A continuación, te hablaré sobre algunos ejemplos de lo que es una sucesión o una progresión geométricas.
En resumen, la fórmula se compone de un término (an) que se obtiene al multiplicar el término anterior (an-1) con un número al cual se le conoce como razón.
Veamos un ejemplo:
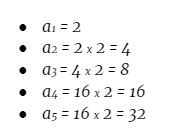
Esta sucesión es geométrica con una razón de r = 2. Así mismo, puede haber diferentes tipos de sucesiones geométricas con otras razones. Solo es cuestión de probar diferentes opciones.
A continuación, encontrarás algunos tipos de operaciones que puedes realizar con las sucesiones. Esto es muy necesario que lo conozcas, y esta es la razón por la cual se explican aquí.
Razón
Tal y como ya hemos mencionado, la razón es ese número constante por el cual se multiplica el término. Si la razón de la progresión geométrica es 5, todos los términos resultantes se multiplicarán por ese número.

Para calcular la razón, es necesario llevar a cabo una sencilla operación matemática. Recordemos que esta es una constante, por lo que, no importa el número de la progresión que elijas, el resultado siempre deberá ser el mismo. La operación para determinarla es la siguiente.
![]()
![]()
Independientemente del término que se elija, el resultado siempre será el mismo y esta será la razón.
Término general
Cuando hablamos de un término general en una sucesión geométrica, este se obtiene a partir del primer término y de la razón.
Con esta operación es posible calcular el término de cualquier parte de la sucesión sin deber tener el resultado de los anteriores.
En este caso, la fórmula sería la siguiente:
![]()
Esta operación en cuestión puede llegar a parecer compleja, pero lo cierto es que es mucho más sencilla de lo que crees.
Así que, no tengas miedo de utilizar esta ecuación para determinar el término general de una progresión geométrica.
Suma de términos
En el caso de que quieras sumar los términos de una progresión geométrica existen dos fórmulas que puedes utilizar. Son fórmulas bastante sencillas pero muy útiles. A continuación, te diremos cuáles son:
La primera fórmula es la siguiente:
![]()
También puedes utilizar la siguiente:
![]()
Indistintamente de cual utilices, el resultado final debería ser el mismo.




